La vida de la adolescente francesa Marie-Sophie Germain quedó marcada para siempre cuando leyó el siguiente relato:
"¡Capturen a Arquímedes!", esa fue la orden dada a los soldados romanos cuando entraron en Siracusa, en la Magna Grecia.
El general Marcelo había ordenado que el matemático fuese llevado ante él.
Pero hubo un soldado a quien no le llegó esa instrucción.
Irrumpió en la casa del extraordinario genio y lo encontró totalmente absorto en un problema de geometría.
Arquímedes estaba haciendo unos dibujos en el suelo y ni se percató de lo que ocurría.
Derechos de autor de la imagenGetty ImagesImage caption Esta ilustración se llama: "La última hora de Arquímedes".
Se volteó hacia el soldado y le dijo: "No toques mis círculos".
El soldado sacó su espada y lo mató.
Era el año 212 a.C.
La fascinación
En plena Revolución Francesa, Germain encontró refugio en la biblioteca de su padre.
Tenía 13 años cuando supo cómo había sido el fin del hombre cuya muerte significó el ocaso de la edad de oro de la matemática griega.
Ilustración de la toma de la Bastilla el 14 de julio de 1789 (Hulton Archive/Getty Images).
"Quedó tan impactada con esa historia que decidió que también quería ser matemática", cuentan en una biografía sobre Germain los profesores John Joshep O'Connor y Edmund Frederick Robertson, de la Universidad St. Andrews, en Reino Unido.
A la joven, nacida en 1776, le sorprendió profundamente ver cómo las matemáticas podían llegar a abstraer a alguien como lo habían hecho con el genio griego, de quien también se cuenta que sus criados tenían que recordarle que comiera y tomara agua.
La autodidacta
Germain era autodidacta y aprendió latín y griego por su cuenta.
En varios países de Europa, durante el siglo XVIII y XIX a las mujeres no se les permitía inscribirse en las universidades para seguir carreras científicas.
En la noche, mientras sus padres dormían, se adentraba en los clásicos de las matemáticas.
Lo hacía entre las cobijas y a veces sus padres apagaban el fuego y le confiscaban las velas e incluso la ropa en un intento por apartarla de los libros.
Pero no pudieron y tuvieron que ceder, y la ayudaron a estudiar por su cuenta porque en su época las mujeres no podían seguir una carrera científica en la universidad.
Y cuando conseguían tutores particulares, estos "se negaban a tomarla en serio", cuenta el autor Simon Singh en un artículo que le dedicó a Germain.
El señor LeBlanc
Cuando cumplió 18 años, Germain tuvo acceso a unos apuntes de las clases que el eminente profesor Joseph-Louis Lagrange impartía en la Escuela Politécnica de París.
Los estudió cuidadosamente y dio un paso inédito: al final del curso le envió un trabajo académico al docente francés y lo firmó con el seudónimo de Monsieur Antoine-August LeBlanc, quien había sido un antiguo alumno de esa institución y había abandonado la ciudad.
decidió escribir a uno de los matemáticos eruditos de la época: Joseph-Louis Lagrange (Ilustración genérica extraída del libro de "The Family Friend", Londres, 1880).
"El profesor estaba muy impresionado porque este estudiante, que no era muy bueno, de repente estaba presentando respuestas extraordinarias y se preguntaba qué había pasado para que se diera semejante transformación. Decidió invitarlo para que hablara sobre sus ideas", le cuenta a BBC Mundo Marcus du Sautoy, autor y profesor de matemáticas de la Universidad de Oxford.
Cuando descubrió que "M LeBlanc" era una mujer, su respeto y admiración por su trabajo quedó intacto y se convirtió en una especie de mentor para ella y ella en una colaboradora a distancia para él.
"Legendre incluyó algunos de sus descubrimientos en un suplemento de la segunda edición de su libro Théorie, indican los profesores de St. Andrews.
El gran Gauss
Tras leer los aportes de Lagendre, Germain decidió estudiar la teoría de los números y se encontró con el trabajo de otra luminaria de las matemáticas de los siglos XVIII y XIX: el alemán Carl Friedrich Gauss, considerado uno de los mejores matemáticos de la historia, si no el más brillante.

El gran Carl Friedrich Gauss, considerado uno de los matemáticos más brillantes de la historia, leyó algunos de los trabajos de Germain y quedó admirado.
Quedó fascinada. Así que nuevamente optó por asumir la identidad del señor LeBlanc para escribirle. Temía que al firmar como mujer fuese ignorada.
En su carta elogiaba su libro Disquisitiones Arithmeticae y le presentaba algunas de sus propias ideas.
"Gauss, por su parte, se mostró complacido con la halagadora correspondencia del talentoso joven M. LeBlanc", cuenta Patricia Rothman, profesora del University College de Londres en su compilado Women in history of mathematics ("Mujeres en la historia de las matemáticas").
Hubo varios intercambios de correspondencia entre ellos.
Una mujer al rescate
"Cuando en 1806, el ejército de Napoleón estaba en conflicto con las fuerzas prusianas, Germain recordó el destino de Arquímedes a manos de los soldados romanos y le pidió a un amigo de la familia, un comandante francés, que enviara a un emisario para proteger a Gauss", indica la autora.
Sophie Germain vivió en la convulsa Francia de finales del siglo XVIII e inicios del siglo XIX.
La ayuda llegó y cuando el militar le dijo a Gauss el nombre de la persona que le había salvado la vida, el gran matemático se mostró muy agradecido y dijo:
"Pero yo no conozco a ninguna Mademoiselle Germain".
Germain tuvo que escribirle para aclarar la situación y "(le dijo que) no era del todo desconocida por él pero 'temiendo el ridículo asociado con una científica femenina' había usado el nombre de M. Le Blanc", recuerda Rothman.
Gauss le expresó su admiración y elogió su talento y genio.
Un problema de más de 300 años
El interés de Germain en la teoría de los números tuvo repercusiones que trascendieron los siglos.
El 1637, el francés Pierre de Fermat escribió una conjetura matemática que hizo que generaciones de matemáticos se rompieran los sesos tratando de dilucidarla.
Una de ellas es su contribución para resolver el Último Teorema de Fermat, uno de los grandes problemas matemáticos que estuvo sin solución por más de 350 años y que finalmente resolvió el profesor de la Universidad de Oxford Andrew J. Wiles.
En 1995, Wiles publicó la respuesta correcta al dilema formulado en 1637 por Pierre de Fermat.
El matemático francés había escrito que no había solución para la ecuación xⁿ + yⁿ = zⁿ, si "n" es un número entero mayor que 2 y "x", "y" y "z" son enteros distintos de cero.
El aporte de Germain
Aunque Germain no lo resolvió en su totalidad, dio un paso importante al formular el teorema que lleva su nombre y demostrar que el Último Teorema de Fermat era cierto para algunos números.
El Último Teorema de Fermat cautivó a Wiles desde que tenía 10 años y no dejó de estudiarlo hasta que dio con la solución.
"Germain logró probar para un particular tipo de ecuaciones que cuando 'n' es un número primo como dos veces ese número primo más 1 también es primo. Por ejemplo, si tomo el (número) primo 5 y lo multiplicó por 2 y le añado 1 es 11, ese también es un número primo. Esos números primos son llamados los números primos Sophie Germain: cuando duplicas un primo y añades 1 el resultado es también un número primo", explica Du Sautoy.
Fue así como nacieron los números primos de Sophie Germain: un número primo p es un número primo de Sophie Germain si 2p + 1 es también un número primo.
Al probar uno de los casos de la enigmática ecuación de Fermat, Germain preparó el terreno para que otros científicos trataran de dilucidarla. Siglos después y tras varios años de dedicarse a ello, Wiles resolvería todos los casos del teorema.
Du Sautoy señala que tomando en cuenta que ha sido "una de las ecuaciones más difíciles de entender" en la historia, la contribución de Germain fue muy significativa, más aún si se consideran las limitaciones que tenían las mujeres de su época.
En el campo de la física
Germain también hizo una importante contribución en el campo de la elasticidad y todo comenzó cuando la Academia de Ciencias de París abrió un concurso en 1809 sobre los experimentos del ingeniero alemán Ernst Chladni.
"Yo le agradecería (a Germain) el haberse convertido en una figura histórica a seguir por desarrollar matemáticas en su nivel más alto", dice Marcus du Sautoy, profesor de la Universidad de Oxford. (Foto: BBC/Big Wave Productions/Mike Cunliffe).
Tras tres intentos (en los que fue la única concursante que se atrevió a presentarse), obtuvo el premio extraordinario de la Academia en 1816 por sus aportes a la teoría dinámica de la curvatura y del comportamiento de las superficies elásticas.
Germain se convirtió en la primera mujer que recibía tal distinción y en la primera a la que se le permitía asistir a las sesiones de esa institución científica, pues sólo a las esposas de sus miembros se les dejaba entrar.
Pero pese a esos reconocimiento, aún sentía que la élite científica no apreciaba sus aportes y siguió trabajando como casi siempre lo hizo: aislada.
Aunque fue Germain la primera que intentó resolver un problema difícil (…) se le dejó por fuera"
Uno de los biógrafos de Sophie Germain
O'Connor y Robertson recuerdan la reflexión de uno de sus biógrafos:
"Aunque fue Germain la primera que intentó resolver un problema difícil, cuando otros con mayor formación, habilidad y con más contactos construyeron sobre la base de su trabajo y cuando la elasticidad se convertía en un tema científico importante, se la dejó por fuera. Las mujeres simplemente no eran tomadas en serio".
Un ícono
Quizás lo que la ciencia más le agradece a Germain no son sus extraordinarios aportes a las matemáticas y la física sino el ejemplo de perseverancia y amor por la ciencia que dio a lo largo de su vida.
Si alguna vez visitas París y te encuentras con una calle como esta... (Foto: Raphael Lorin)

estarás caminado por la calle Sophie Germain (Foto: Raphael Lorin).
"Aún estamos luchando contra el estereotipo de que las matemáticas es un campo dominado por hombres. Lo más importante para que las mujeres entren en este ámbito de la ciencia es tener modelos a seguir. Hoy en día contamos con muchos (…) pero tener figuras históricas como Germain es extremadamente importante. Por eso hay que celebrar su vida y sus contribuciones. Eso es lo que yo le agradecería: haberse convertido en una figura histórica a seguir por desarrollar matemáticas en su nivel más alto", indica el profesor Du Sautoy.
Germain no se casó ni tuvo hijos. Se entregó a las matemáticas como lo hiciera el Arquímedes que la marcó en su niñez.
Murió en 1831, tras sufrir cáncer de seno.
Su certificado de defunción no la identificaba como profesional, matemática o científica sino como "rentier" (rentista).
El doctorado honoris causa que Gauss pidió para ella en vida, se lo acabó concediendo la Universidad de Gotinga tras su muerte.
Con los años se convirtió en un ícono de las matemáticas.
La Academia de Ciencias de Francia concede anualmente el Premio Sophie Germain a los matemáticos que hacen importantes contribuciones a ese campo.
Muchos se preguntan cuántos aportes de Germain quizás siguen escondidos en las tantas cartas que escribió con la firma de Monsieur Antoine-August LeBlanc.
 Derechos de autor de la imagenGetty ImagesImage caption A los 81 años, el canadiense Robert Langlands sigue trabajando en el Instituto de Estudios Avanzados de Princeton.
Derechos de autor de la imagenGetty ImagesImage caption A los 81 años, el canadiense Robert Langlands sigue trabajando en el Instituto de Estudios Avanzados de Princeton. 






















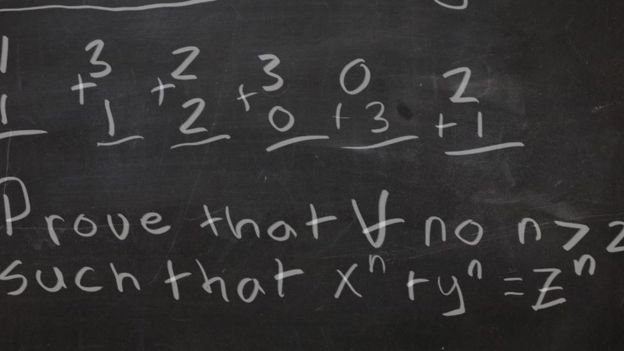



 estarás caminado por la calle Sophie Germain (Foto: Raphael Lorin).
estarás caminado por la calle Sophie Germain (Foto: Raphael Lorin). 